RSA算法解释

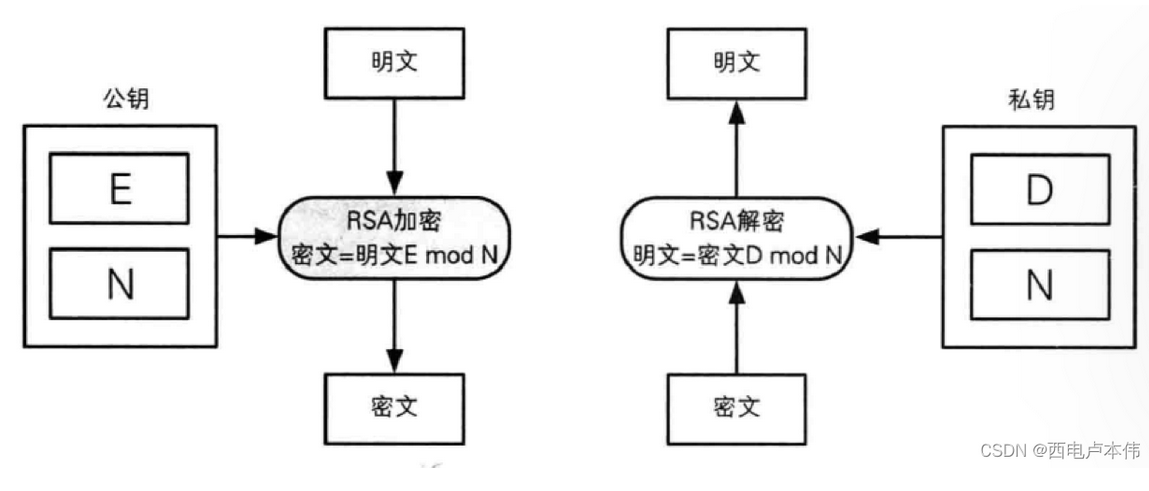
加密算法
$$
c≡ m^e (mod N)
$$
其中c 作为密文 m 作为明文

也就是说在 e 与 N 作为 RSA加密算法的公钥 也就是 (E,N) 公钥可公开

解密算法
$$
m ≡ c^d (mod N)
$$
也就是说 RSA的明文就是代表密文字符 c的 d次方对N求余的结果 那么这里的 (d ,N) 便作为 私钥

其实这里你也许已经发现了 既然公钥与私钥之中都存在有N 那么N不就是代表 公开的吗 那么其中主要保存的其实就是 e(encode 编码) 与 d (decode 解码)

image-20220906162155058

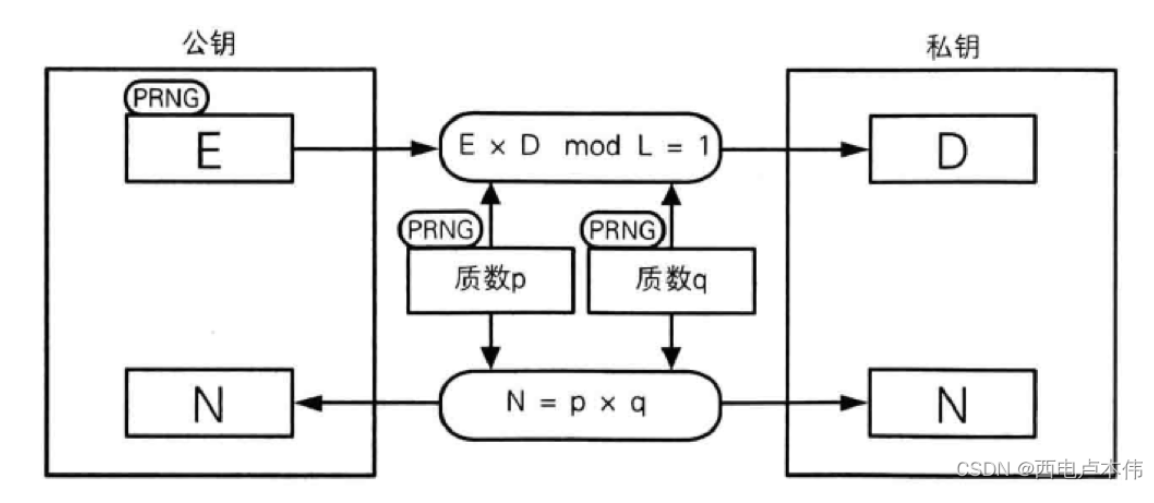
生成密钥对

由上面可知 我们生成密钥对的时候需要三个参数 e d n 那么怎么生成呢?

求 N

首先需要准备两个极大的指数 P Q
$$
P * Q = N
$$
这样得到了N

求 φ

$$
φ = (P -1 )* (Q - 1)
$$

φ 为啥要这么求?

求E

e的求解基于上述的 φ 值 首先需要明确 e的取值范围 1 < e < φ ,并且 gcd(φ , e) = 1(即φ 与e的最大公约数为1,即两者互质) 之所以需要添加1 这个值 ,是为了保证存在解密时需要使用的参数 D

求 D

首先需要明确 d 的取值范围 1 < d < φ ,并且 gcd(φ , d) = 1
$$
e * d (mod φ) =1
$$
image-20220906162206289

举例

求n

这里取两个素数 p = 3 q = 11

n= 33

求 φ

$$
φ = (3-1)*(11-1) = 20
$$

求e

gcd(φ,e) = 1 也就是需要找一个数与20 互质

3,7,11,13,17,19 这里选择三

那么我们得到了 e = 3

求d

$$
e * d (mod φ) = 1 3 * 7 / 20 …..余 1
$$

因此d = 7

加密

需要加密的明文必须是小于n的,也就是小于33的数 这里便随便取一下为5
$$
c = m ^e (mod N) = 5^3 (mod 33) = 75 / 33 …余 26 = 26
$$
因此 c 就是26 那么密文就是26

解密

$$
m = c^d (mod N) = 26^7(mod 33) = 5
$$

常见的大整数n的分解方法

对于上面的 的 数值 其中 公钥 e 与 公共模数 n其实都是我们已知的 ,那么反过来我们需要用 n去获取 p q 也就是两个 质数 还记得 我们是怎么获取的n 吗

n = p * q

如果我们现在已经获取了 p 和 q 那么下面的过程就跟正常加密属于一样的了

如何进行大整数n的分解呢?

  1. 当n的长度较小的时候,采取爆破
  2. 当n满足 因数p q 相差较小 或 相差很大时 ,可以采用离线工具 yafu来分解
  3. 当 n 的位数过大是,并且不满足上述条件,可以采用在线网站 factordb ,改网站类似于彩虹表,将已经被分解的大数的结果存储起来 只需要进行查询

那么可以发现其实并没有一个特别好的方法破解

逆元

还记得上面求解私钥指数d 的公式吗
$$
e * d (mod φ) = 1
$$
这个公式也可以写成
$$
e * d ≡ 1(mod φ)
$$
≡ 代表同余

定义

如果一个线性同余方程 ax ≡ 1(mod b),则 x 称为 a(mod b) 的逆元 记作a^-1^ ,一个数有逆元的充分必要条件是 gcd(a,b) = 1 ,此时逆元唯一存在

此处为什么要讨论逆元,其一rsa中有逆元的概念,其二,中国剩余定理(CRT) 可与rsa算法结合来进行加解密,crt又逃不开逆元的概念.

那么上面的求解私钥指数d,可以说e的逆元是d(mod φ)

费马小定理

如果p是一个指数,而整数a不是p的倍数,则

a^p-^^1^ ≡ (mod p)

可得

a * a^p^^-^^2^ ≡ 1(mod p)

那么根据逆元的定理 得到 a的逆元即为 a^p^^-^^2^ (mod p)

快速幂算法

https://blog.csdn.net/weixin_44002938/article/details/103427778 写的不错

思想

3^10 = 3*3*3*3*3*3*3*3*3*3
3^10 = (3 * 3) ^ 5
3^ 10 = 9^5
此时的指数有10缩短了一半变成了5,而低于变成了原来的平法,求3^10原本需要执行10此虚幻操作,而求 9^5却只需要执行5此循环操作,特别是在幂特别大的时候效果非常好,例如2^1000 = 4^500,底数仅仅做了一个小小的平方操作,而指数就从1000变成看500,减少了500次
但是我们如果来看9^5 这样就变成了一个奇数 ,当再次减少一半的时候指数就变成了 2.5 那么我们肯定不能直接减少一半了

9^5 = (9^4) * (9^1)
这样指数就又变成了偶数了

扩展欧几里得

逆元的含义决定了 ax ≡ 1(mod b) 等价于ax = kb + 1

中国剩余定理(CRT) 加速rsa算法

https://www.cnblogs.com/MashiroSky/p/5918158.html

在《孙子算经》中有这样一个问题：“今有物不知其数，三三数之剩二（除以3余2），五五数之剩三（除以5余3），七七数之剩二（除以7余2），问物几何？”这个问题称为“孙子问题”，该问题的一般解法国际上称为“中国剩余定理”。具体解法分三步：
  1. 找出三个数 从3 和 5的公倍数中找出被7除余1的最小数15 ,从 3和 7的公倍数中找出被5除余1的最小数21,最后从5和7的公倍数中找出除3余1的最小数70
  2. 用15乘以2(2为最终结果除以7的余数),用21乘以3(3为最终结果除以5的余数),同理,用70乘以2(2为最终结果除以3的余数),然后把三个乘积相加 15 * 2 + 21 * 3 + 70 * 2 得到和233
  3. 用233除以3,5,7三个数的最小公倍数105,得到余数23,即 233 % 105 = 23 .这个余数23就是符合条件的最小数.

首先我们假设n1 是满足除以3余2的一个数,比如2,5,8 等等,也就是满足3 * k + 2 (k >= 0)的一个任意数.同时 我们假设n2 是满足除以5与3的一个数,n3 是满足除以7余2的一个数

我们先从n1 这个角度出发,一直n1满足除以3除2的一个数,比如2,5,8等等,也就是满足3 * k + 2 (k > = 0) 的一个任意数,同样我们假设n2 是满足除以5 余3的一个数,n3是满足除以7余2的一个数

我们先从n1 这个角度出发,已知 n1 满足除以3余2,能不能是得 n1 + n2 的和人满足除以3 余 2 进而使得 n1 + n2 + n3 的和人满足除以3 余 2

这就涉及了一个基本的数学定理,如果有 a% b = c 则有 (a + k * b) % b = c(k为非零整数),换句话说,如果一个出发运算的除数为c ,那被除数与k倍的除数相加(或者相减) 的和 (差) 再与除数相除,余数不变,

那么 如果n2 是3的倍数, n1 + n2 就依然满足除以3余2 同理,如果n3 也是3 的倍数,那么n1 + n2 + n3 的和就满足除以3 余 2

  1. 为使n1 + n2 + n3 的和满足除以3余2,n2 和n3必须是3的倍数
  2. 为使n1 + n2 + n3 的和满足除以5余3 , n1和n3必须是3的倍数
  3. 为使n1 + n2 + n3 的和满足除以7余3 , n1和n2必须是7的倍数

孙子问题解法的本质是从5和7的公倍数中找到一个除以3 余 2的数n1 ,从3和7的公倍数中找到一个除以5余3的数n2 ,从 3和 5的公倍数中找到一个除以7余2的数 n3 在将三个数相加得到解,在n1 n2 n3 时又用了一个小技巧,以n1为例,并非从5和7的公倍数中直接找到一个除以3余2的数,先是找到一个除以3余1 的数,在乘以2.就是先求出5和7的公倍数模3下的逆元,在用逆元去乘余数

最后我们还要清楚一点 n1 + n2 + n3 只是问题的一个解,并不是最小的解,如何求解最小的解,我们只需要从中最大限制的减掉3,5,7的公倍数105即可

这样便得到了中国剩余定理

设正整数m1,m2 , … , mk
x ≡ a1(mod m1)
x ≡ a2(mod m2)
x ≡ a3(mod m3)
.
.
.
x ≡ ak (mod mk)

有整数解,并且在模M=m1 * m2 * … *mk 下的解是唯一的

x ≡ (a1 M1 M1^-^^1^ + a2M2 M2^-^^2^ + … + akMk Mk^-^^k^)mod M

其中Mi = M/mi 而Mi^-^^1^ 为Mi 模mi 的逆元

中国剩余定理扩展 - 求解模数不互质情况下的线性方程组

普通的中国剩余定理要求所有的mi 互素,那么如果不互素呢

这种情况就需要采用两两合并的思想,假设要合并如下的两个方程
x = a1 + m1 x1
x = a2 + m2 x2

那么得到
$$
a_1+m_1x_1 = a_2 + m_2x_2 => m_1x_1 + m_2x_2 = a_2-a_1
$$
​ 我们需要求出一个最小的x使他满足
$$
x = a_1 + m_1x_1 = a_2 + m_2x_2
$$
那么x1 和x2 就要尽可能的小,于是我们用扩展欧几里得算法求出x1 的最小正整数解,将它待会a1 + m1 x1 得到x的一个特解x^’^ ,当然也是最小正整数解,所以x的通解一定是x′加上lcm(m1,m2)∗k，这样才能保证x模m1和m2的余数是a1和a2。由此，我们把这个x′当做新的方程的余数，把lcm(m1,m2)当做新的方程的模数。（这一段是关键）lcm最小公倍数

x ≡ x^’^ (mod lcm(m1 ,m2))

简化

降N

由中国剩余定理可知,设p和q是相互独立的大素数,n为p*q,对于任意的(m1 , m2) ,且 0 <= m1 < p 0 <= m2 < q,必然存在一个唯一的m,0 <= m <n
m1 = m (mod p)
m2 = m (mod q)

换句话说,给定一个(m1,m2),其中满足上述等式的m必定唯一存在.所以解密RSA的流程为m = c ^d^ (mod n),可以分解为
m1 = c^d^ (mod p)
m2 = c^d^ (mod q)

然后在计算m, 但是等式c^d (mod p) 或者c^d^ (mod q),模数虽然从n降为p或q了.但是私钥指数d还是比较大,我们还是需要将低指数

降d

仔细看等式c^d^ (mod p)

令d = k(p-1) + r 则 c^d^ (mod p)
= c^k^^(^^p^^-^^1^^)^^+^^r^ (mod p)
= c^r^ * c^k^^(^^p^^-^^1^^)^ (mod p)
因为c^(^^p^^-^^1^^)^(mod p) =1
=c^r^ (mod p)

r是d除 p-1的余数,即r = d(mod (p-1)) 所以c^d^ (mod p) 可以降价为 c ^d^ ^m^^o^^d^ ^p^^-^^1^ (mod p)
dp = d mod p-1
dq = d mod q-1

这样 m1 和 m2 就降为
m1 = c^d^^p^ mod p
m2 = c^d^^q^ mod q

解密

模数都降的差不多了。想要求解明文，除了上述的 p、q、d、dp、dq，我们还需要 q 对 p 的逆元

qinv = q ^-^^1^ mod p

最后得到的明文公式

h = qinv(m1−m2) mod p
m = m2=+hq mod p∗q